إصلاح التمارين 12-13-14-15-16 صفحة 187 - إصلاح كتاب الرياضيات السنة السابعة أساسي

المثلثّات

أنشطة بناء مثلّثات

إصلاح التمرين رقم 12 صفحة 187

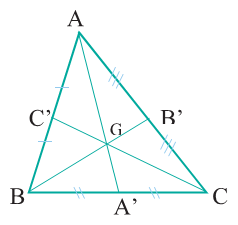
أ) مساحة المثلّث \(GA'B\) هو (الارتفاع × القاعدة) ÷ 2، يعني

\(\frac{GH\times BA'}{2}\)

كما في الصورة

ومساحة المثلّث \(GA'C\) هو (الارتفاع × القاعدة) ÷ 2، يعني

\(\frac{GH\times A'C}{2}\)

وبما أنّ \(BA'=A'C\) فهذا يعني أنّ مساحة المثلّث \(GA'B\) تساوي مساحة المثلّث \(GA'C\).

ب) المثلّثان \(GAB\) و\(GAC\) لهما نفس المساحة لأنّ لهما نفس القاعدة \(AG\) ونفس الارتفاعين الصادرين من النقطة \(B\) والنقطة \(C\) وهذا لأنّنا علمنا أنّ المثلثين \(GA'B\) و\(GA'C\) لهما نفس المساحة.

ج) المثلّثان \(GAB\) و\(GBC\) لهما نفس المساحة لأنّ لهما نفس القاعدة \(GB\) ونفس الارتفاعين الصادرين من النقطة \(A\) والنقطة \(C\) وهذا لأنّنا علمنا أنّ المثلثين \(GA'B\) و\(GA'C\) لهما نفس المساحة.

وعليه نستنتج أنّ المثلثات مساحاتها متساوية وبالتالي فإنّ انجاز المهندس كان صحيحا.

إصلاح التمرين رقم 13 صفحة 187

أ) لدينا \(HI\) تقطع المثلّث \(HEK\) إلى مثلثين متساويين في المساحة وبالتالي فإنّ مساحة \(HIK\) تساوي نصف مساحة المثّلث \(HEK\).

مساحة المثلّث \(HEK\) هي :

\(\frac{HE\times HK}{2}=\)

\(\frac{3\times 4}{2}=\)

\(\frac{12}{2}=6\)

ومساحة \(HIK\) هي 

\(\frac{6}{2}=3~cm^2\)

ب) لدينا 

\(\frac{HI\times IK}{2}=3\)

\(HI\times 2,5=6\)

\(HI=\frac{6}{2,5}\)

\(HI=2,4\)

ج) مساحة الرباعي \(KHIR\) هي مساحة المثلّث \(HIK\) + مساحة المثلّث \(KIR\).

مساحة المثلّث \(HIK\) تساوي \(3\).

ومساحة المثلّث \(KIR\) تساوي :

\(\frac{KR\times IK}{2}=\)

\(\frac{12\times 2,5}{2}=\)

\(\frac{30}{2}=15\)

وبالتالي مساحة \(KHIR\) تساوي :

\(3+15=18~cm^2\)

إصلاح التمرين رقم 14 صفحة 187

أ) نقوم برسم الموسّط العمودي لقطعة المستقيم \([AB]\) ونعين نقطة التقاطع بينه وبين المستقيم \(\Delta\)، هذه النقطة نسميها \(E\)، وهي القمة الرئيسة للمثلّث \(EAB\)، كما في الصورة :

وبطبيعة الحال لا توجد إلاّ إمكانية واحدة لأنّ كلّ قطعة مستقيم لديها موسّط عمودي واحد لا غير.

ب) لا يمكن إنجاز نفس العمل إذا كان المستقيم \((AB)\) عمودي على المستقيم \(\Delta\) لأنّ المنصّف العمودي لقطعة المستقيم \([AB]\) سيكون موازي لـ\(\Delta\) ولا يتقاطعان أبدا.

ج) 

توجد إمكانيتين في هذه الحالة كما في الصورة

الدائرة التي مركزها النقطة \(C\) وشعاعها \(CD\) تقطع المستقيم \(\Delta\) في النقطتين.

إصلاح التمرين رقم 15 صفحة 187

في هذا الرسم القمّة الرئيسيّة للمثلّث هي \(K\) كما في الصورة :

وهذا خطأ، وكان يجب عليه كما هو مطلوب في التمرين أن تكون قمّة المثلّث هي النقطة \(R\) كما في الصورة :


إصلاح التمرين رقم 16 صفحة 187

عودة إلى صفحة إصلاح كتاب الرياضيات السنة السابعة أساسي