إصلاح التمارين 9-10-11-12-13-14-15-16 صفحة 108 - إصلاح كتاب الرياضيات السنة السابعة أساسي

الأعداد العشريّة - الأعداد الكسريّة

إصلاح التمرين رقم 9 صفحة 108

\(500\times \frac{12400000}{10^3}=\)

\(500\times \frac{12400\times10^3}{10^3}=\)

\(500\times12400=\)

\(6200000\)

\(10^2\times 3,2\times0,01=\)

\(10^2\times 3,2\times \frac{1}{10^2}=\)

\(3,2\)

\(2,5\times80\times10^9\times 0,00001=\)
\(2,5\times80\times10^9\times \frac{1}{10^5}=\)
\(2,5\times80\times10^4=\)
\(2000000\)

\(2,001\times300\times10^4=\)
\(\frac{2001}{10^3}\times300\times10^4=\)
\(2001\times300\times10=\)
\(6003000\)


إصلاح التمرين رقم 10 صفحة 108

إصلاح التمرين رقم 11 صفحة 108

أ) نرتّب الأعداد العشريّة النسبيّة تصاعديّا (من الأصغر إلى الأكبر) :

\(20>5,6>1,9>0,9>0>-1>-4>-4,7>-5>-18\)

ب) الأعداد الصحيحة النسبية من بين هذه المجموعة هي :

\(20;0;-1;-4;-5;-18\)

ج) 

إصلاح التمرين رقم 12 و13 صفحة 108

أ) حتّى نتمكّن من تحديد فواصل هذه النقاط، يجب علينا أن نعرف الوحدة التي أقيم بها هذا المدرّج. ولو لاحظنا مكان الرقم \(1\) لوجدنا أنّ هناك \(4\) مربعات صغيرة، يعني كلّ \(4\) مربعات تساوي \(1\). وبالتالي :

* النقطة \(A\) فاصلتها \(-1\) لأنّها موجودة قبل \(4\) مربعات من الـ\(0\) ولهذا فهي سالبة.

* النقطة \(B\) فاصلتها \(0,5\) لأنّها موجودة بعد \(2\) مربعات من الـ\(0\) ولهذا فهي موجبة.

* النقطة \(C\) فاصلتها \(2,5\) لأنّها موجودة بعد \(10\) مربعات من الـ\(0\) ولهذا فهي موجبة.

* النقطة \(D\) فاصلتها \(-1,5\) لأنّها موجودة قبل \(6\) مربعات من الـ\(0\) ولهذا فهي سالبة.

ب) النقطة \(I\) فاصلتها \(1,5\) يعني \(6\) مربعات بعد الصفر.

والنقطة \(J\) فاصلتها \(-2,5\) يعني \(10\) مربعات قبل الصفر.

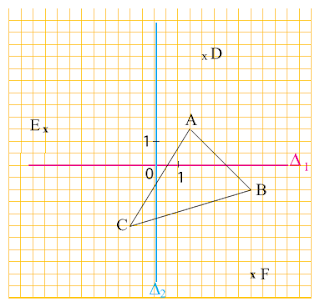
إصلاح التمرين رقم 14 صفحة 108

أ) \(2\) مربعات تساوي \(1\). وبالتالي :

- إحداثيّات النقطة \(A\) هي \(3\) مربعات أفقي (محور الفواصل) و\(3\) مربعات عمودي (محور التراتيب) يعني \((1,5;1,5)\).

- إحداثيّات النقطة \(B\) هي \(8\) مربعات أفقي (محور الفواصل) و\(-2\) مربعات عمودي (محور التراتيب) يعني \((-1;4)\).

- إحداثيّات النقطة \(C\) هي \(2\) مربعات أفقي (محور الفواصل) و\(-5\) مربعات عمودي (محور التراتيب) يعني \((-2,5;-1)\).

ب)

ج) - إحداثيّات النقطة \(A'\) هي \(-3\) مربعات أفقي (محور الفواصل) و\(3\) مربعات عمودي (محور التراتيب) يعني \((1,5;-1,5)\).

- إحداثيّات النقطة \(B'\) هي \(-8\) مربعات أفقي (محور الفواصل) و\(-2\) مربعات عمودي (محور التراتيب) يعني \((-1;-4)\).

- إحداثيّات النقطة \(C'\) هي \(2\) مربعات أفقي (محور الفواصل) و\(-5\) مربعات عمودي (محور التراتيب) يعني \((-2,5;1)\).

د) \(B\) و \(F\) لهما نفس الفاصلة.

هـ) \(A\) و\(A'\) و\(E\) لهم نفس الترتيب.

\(C\) و \(C'\) لهما نفس الترتيب.

\(B\) و \(B'\) لهما نفس الترتيب.

إصلاح التمرين رقم 15 صفحة 108

رشاد وأصدقائه الأربع، \(5\) أشخاص. يعني سنقوم بقسمة لترين من العصير على خمسة أشخاص فيتحصّل كلّ واحد منهم على :

\(\frac{2}{5}=0,4\)

.لتر

إصلاح التمرين رقم 16 صفحة 108

أ)

\(AI=\frac{AB}{2}\)
\(AI=\frac{1}{2}AB\)

ب)

\(AK=\frac{AI}{2}\)

\(AK=\frac{\frac{AB}{2}}{2}\)

\(AK=\frac{AB}{4}\)

\(AK==\frac{1}{4}AB\)

ج)

لدينا

\(AK=\frac{1}{4}AB\)

وهذا يعني

\(AB=4AK\)

ولدينا أيضا

\(AK+BK=AB\) \(\Rightarrow\)
\(AK+BK=4AK\) \(\Rightarrow\)
\(AK-4AK=-BK\) \(\Rightarrow\)
\(-3AK=-BK\) \(\Rightarrow\)
\(3AK=BK\) \(\Rightarrow\)
\(AK=\frac{BK}{3}\) \(\Rightarrow\)
\(AK=\frac{1}{3}BK\)

عودة إلى صفحة إصلاح كتاب الرياضيات السنة السابعة أساسي